Programación Dinámica

Programación Dinámica II

Cambio de moneda: Numero de formas

Enunciado

Dado un array coinValue con las denominaciones de las monedas, de tamaño N:


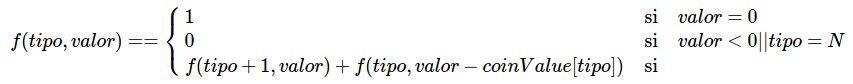
private static int N = 5;
private static int[] coinValue = new int[] {1, 5, 10, 25, 50};
private static int[][] memo = new int[6][7500]; //Inicializar a -1

private static int ways(int type, int value) {
  
}


private static int N = 5;
private static int[] coinValue = new int[] {1, 5, 10, 25, 50};
private static int[][] memo = new int[6][7500]; //Inicializar a -1

private static int ways(int type, int value) {
  if (value == 0)              return 1;
  if (value < 0 || type == N)  return 0;
}


private static int N = 5;
private static int[] coinValue = new int[] {1, 5, 10, 25, 50};
private static int[][] memo = new int[6][7500]; //Inicializar a -1

private static int ways(int type, int value) {
  if (value == 0)              return 1;
  if (value < 0 || type == N)  return 0;
  return ways(type + 1, value) + ways(type, value - coinValue[type]);
}


private static int N = 5;
private static int[] coinValue = new int[] {1, 5, 10, 25, 50};
private static int[][] memo = new int[6][7500]; //Inicializar a -1

private static int ways(int type, int value) {
  if (value == 0)              return 1;
  if (value < 0 || type == N)  return 0;
  if (memo[type][value] != -1) return memo[type][value];
  memo[type][value] = ways(type + 1, value) + ways(type, value - coinValue[type]);
  return memo[type][value];
}

Tabla

Version bottom - up


private static int N = 5, M = 12;
private static int[] coinValue = new int[] {1, 5, 10, 25, 50};
private static int[][] memo = new int[N][M];
	
public static void ways() {
  for(int i = N - 1; i >= 0; i--) { // i = tipo actual
    for(int j = 0; j < M; j++) { // j = valor actual
    }
  }
}

Version bottom - up


private static int N = 5, M = 12;
private static int[] coinValue = new int[] {1, 5, 10, 25, 50};
private static int[][] memo = new int[N][M];
	
public static void ways() {
  for(int i = N - 1; i >= 0; i--) { // i = tipo actual
    for(int j = 0; j < M; j++) { // j = valor actual
      if (j == 0) {
        memo[i][j] = 1;
      } 
    }
  }
}

Version bottom - up


private static int N = 5, M = 12;
private static int[] coinValue = new int[] {1, 5, 10, 25, 50};
private static int[][] memo = new int[N][M];
	
public static void ways() {
  for(int i = N - 1; i >= 0; i--) { // i = tipo actual
    for(int j = 0; j < M; j++) { // j = valor actual
      if (j == 0) {
        memo[i][j] = 1;
      } else {
        int valor1 = 0, valor2 = 0, _i, _j;
        // Calculamo valor1, es decir, posibilidad de no incluir la moneda
        _i = i + 1;
        _j = j;
        if(_i < N) valor1 = memo[_i][_j];
        
      }
    }
  }
}

Version bottom - up


private static int N = 5, M = 12;
private static int[] coinValue = new int[] {1, 5, 10, 25, 50};
private static int[][] memo = new int[N][M];
	
public static void ways() {
  for(int i = N - 1; i >= 0; i--) { // i = tipo actual
    for(int j = 0; j < M; j++) { // j = valor actual
      if (j == 0) {
        memo[i][j] = 1;
      } else {
        int valor1 = 0, valor2 = 0, _i, _j;
        // Calculamo valor1, es decir, posibilidad de no incluir la moneda
        _i = i + 1;
        _j = j;
        if(_i < N) valor1 = memo[_i][_j];
				
        // Calculamos valor2, es decir, posibilidad de incluir la moneda
        _i = i;
        _j = j - coinValue[_i];
        if(_j >= 0) valor2 = memo[_i][_j];			
        
      }
    }
  }
}

Version bottom - up


private static int N = 5, M = 12;
private static int[] coinValue = new int[] {1, 5, 10, 25, 50};
private static int[][] memo = new int[N][M];
	
public static void ways() {
  for(int i = N - 1; i >= 0; i--) { // i = tipo actual
    for(int j = 0; j < M; j++) { // j = valor actual
      if (j == 0) {
        memo[i][j] = 1;
      } else {
        int valor1 = 0, valor2 = 0, _i, _j;
        // Calculamo valor1, es decir, posibilidad de no incluir la moneda
        _i = i + 1;
        _j = j;
        if(_i < N) valor1 = memo[_i][_j];
				
        // Calculamos valor2, es decir, posibilidad de incluir la moneda
        _i = i;
        _j = j - coinValue[_i];
        if(_j >= 0) valor2 = memo[_i][_j];			
        memo[i][j] = valor1 + valor2;
      }
    }
  }
  // No retorno
}

Cambio de moneda

Dada una cantidad V de centavos, y una lista de n monedas existentes, determinar cual es la mínima cantidad de monedas que debe usarse para completar V.

Sub-estructura óptima.
Superposición de Problemas.

Planteamiento

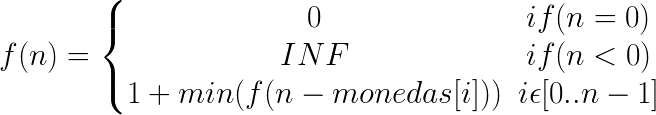
Solución Recursiva


INTEGER monedas[]

INTEGER change(INTEGER k) {
    IF (k == 0) 
        RETURN 0
    IF (k < 0)
        RETURN INF
    INTEGER rta = INF
    FOR i IN RANGE[0, n - 1]
        rta = MIN(rta, change(k - monedas[i]))
    RETURN rta + 1
}

Añadiendo tabla DP


INTEGER monedas[n]
INTEGER memo[n] //Se inicializa en -1 o NULL

INTEGER change(INTEGER k) {
    IF (k == 0) 
        RETURN 0
    IF (k < 0)
        RETURN INF
    INTEGER rta = INF
    FOR i IN RANGE[0, n - 1]
        rta = MIN(rta, change(k - monedas[i]))
    RETURN rta + 1
}

Verificando si ya ha sido calculado


INTEGER monedas[n]
INTEGER memo[MAX] 

INTEGER change(INTEGER k) {
    IF (k == 0) 
        RETURN 0
    IF (k < 0)
        RETURN INF
    IF (memo[k] != -1)
        RETURN memo[k]
    INTEGER rta = INF
    FOR i IN RANGE[0, n - 1]
        rta = MIN(rta, change(k - monedas[i]))
    RETURN rta + 1
}

Calculando y guardando


INTEGER monedas[n]
INTEGER memo[MAX] 

INTEGER change(INTEGER k) {
    IF (k == 0) 
        RETURN 0
    IF (k < 0)
        RETURN INF
    IF (memo[k] != -1)
        RETURN memo[k]
    INTEGER rta = INF
    FOR i IN RANGE[0, n - 1]
        rta = MIN(rta, change(k - monedas[i]))
    memo[k] = rta + 1
    RETURN rta + 1
}

Problema de la Mochila

Dada una mochila con una capacidad W, y n productos, donde cada producto tiene un peso wi y un valor vi, calcular el mayor valor que puede introducirse en la mochila, sin exceder su capacidad.

Sub-estructura óptima.
Superposición de Problemas.

Planteamiento

Dados:

W[n] => Pesos de los n productos
P[n] => Valor de los n productos

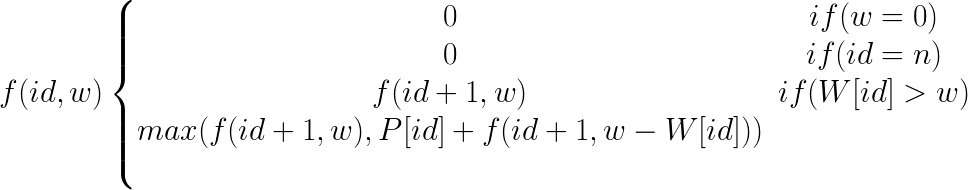
Solución Recursiva sin memorización


INTEGER N //Numero de objetos 
INTEGER prices[] //precios de cada producto
INTEGER weights[] //pesos de cada producto

INTEGER knapsack(INTEGER id, INTEGER w) {
    IF (id == N || w == 0) 
        RETURN 0
    IF (weights[id] > w)
        RETURN knapsack(id + 1, w)
    ELSE
        RETURN MAX(knapsack(id + 1, w), prices[id] + knapsack(id + 1, w - weights[id]))
}

Añadimos tabla DP


INTEGER N //Numero de objetos 
INTEGER prices[] //precios de cada producto
INTEGER weights[] //pesos de cada producto
INTEGER memo[][] //DEBE INICIALIZARSE EN -1 y/o null

INTEGER knapsack(INTEGER id, INTEGER w) {
    IF (id == N || w == 0) 
        RETURN 0
    IF (weights[id] > w)
        RETURN knapsack(id + 1, w)
    ELSE
        RETURN MAX(knapsack(id + 1, w), prices[id] + knapsack(id + 1, w - weights[id]))
}

Verificamos si el problema ya se precalculó


INTEGER N //Numero de objetos 
INTEGER prices[] //precios de cada producto
INTEGER weights[] //pesos de cada producto
INTEGER memo[][] 

INTEGER knapsack(INTEGER id, INTEGER w) {
    IF (id == N || w == 0) 
        RETURN 0
    IF (memo[id][w] != -1) 
        RETURN memo[id][w]
    IF (weights[id] > w)
        RETURN knapsack(id + 1, w)
    ELSE
        RETURN MAX(knapsack(id + 1, w), prices[id] + knapsack(id + 1, w - weights[id]))
}

Precalculamos y guardamos


INTEGER N //Numero de objetos 
INTEGER prices[] //precios de cada producto
INTEGER weights[] //pesos de cada producto
INTEGER memo[][] 

INTEGER knapsack(INTEGER id, INTEGER w) {
    IF (id == N || w == 0) 
        RETURN 0
    IF (memo[id][w] != -1) 
        RETURN memo[id][w]
    IF (weights[id] > w)
        memo[id][w] = knapsack(id + 1, w)
    ELSE
        memo[id][w] =  MAX(knapsack(id + 1, w), prices[id] + knapsack(id + 1, w - weights[id]))
}

Precalculamos y guardamos


INTEGER N //Numero de objetos 
INTEGER prices[] //precios de cada producto
INTEGER weights[] //pesos de cada producto
INTEGER memo[][] 

INTEGER knapsack(INTEGER id, INTEGER w) {
    IF (id == N || w == 0) 
        RETURN 0
    IF (memo[id][w] != -1) 
        RETURN memo[id][w]
    IF (weights[id] > w)
        memo[id][w] = knapsack(id + 1, w)
    ELSE
        memo[id][w] =  MAX(knapsack(id + 1, w), prices[id] + knapsack(id + 1, w - weights[id]))
    RETURN memo[id][w]
}

Ejercicios propuestos

UFPS - Week 3