Programación Dinámica
Top - down
Programación Dinámica
El método de programación dinámica sirve para resolver problemas combinando las soluciones de subproblemas. Normalmente es usada para resolver problemas de optimización.
Condiciones
- Sub-estructura óptima. Un problema tiene sub-estructura óptima cuando la solución óptima a un problema se puede componer a partir de soluciones óptimas de sus sub-problemas.
- Superposición de Problemas. El cálculo de la solución óptima implica resolver muchas veces un mismo sub-problemas. La cantidad de sub-problema es “pequeña”.
DP = Recursión + Memorización
Recursión: Sucesión de fibonacci
0,1,1,2,3,5,8,13,21,34,55,89,144
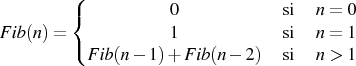
FUNCTION fibonacci(INTEGER n)
IF (n < 2)
RETURN n
ELSE
RETURN fibonacci(n - 1) + fibonacci(n - 2)
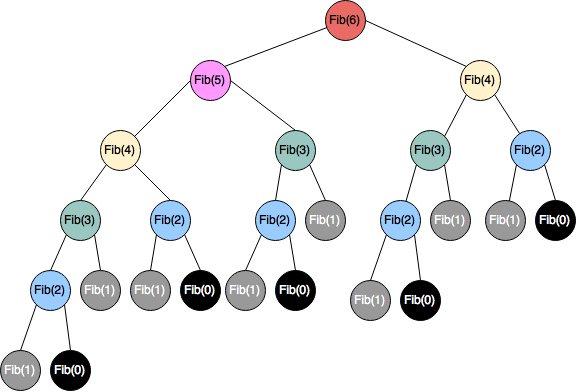
Memorización: Sucesión de fibonacci
ARRAY[n + 1] terminos
FUNCTION fibonacci()
IF(n < 2)
RETURN n
ELSE
terminos[0] = 0
terminos[1] = 1
FOR(INTEGER i IN RANGE [2, n])
terminos[i] = terminos[i - 1] + terminos[i - 2]
Programación Dinámica
ARRAY[n + 1] terminos
FUNCTION fibonacci(INTEGER i)
IF(terminos[i] != 0)
RETURN terminos[i]
IF(n < 2)
terminos[i] = n
ELSE
terminos[i] = fibonacci(i - 1) + fibonacci(i - 2)
RETURN terminos[i]
*Código con fines ilustrativos. Formas mas eficiente de calcular Fibonacci aqui
Problema de la Mochila
Dada una mochila con una capacidad W, y n productos, donde cada producto tiene un peso wi y un valor vi, calcular el mayor valor que puede introducirse en la mochila, sin exceder su capacidad.
- Sub-estructura óptima.
- Superposición de Problemas.
Planteamiento
Dados:
- W[n] => Pesos de los n productos
- P[n] => Valor de los n productos
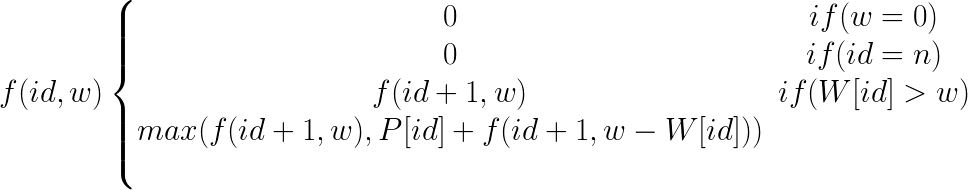
Solución Recursiva sin memorización
INTEGER N //Numero de objetos
INTEGER prices[] //precios de cada producto
INTEGER weights[] //pesos de cada producto
INTEGER knapsack(INTEGER id, INTEGER w) {
IF (id == N || w == 0)
RETURN 0
IF (weights[id] > w)
RETURN knapsack(id + 1, w)
ELSE
RETURN MAX(knapsack(id + 1, w), prices[id] + knapsack(id + 1, w - weights[id]))
}
Añadimos tabla DP
INTEGER N //Numero de objetos
INTEGER prices[] //precios de cada producto
INTEGER weights[] //pesos de cada producto
INTEGER memo[][] //DEBE INICIALIZARSE EN -1 y/o null
INTEGER knapsack(INTEGER id, INTEGER w) {
IF (id == N || w == 0)
RETURN 0
IF (weights[id] > w)
RETURN knapsack(id + 1, w)
ELSE
RETURN MAX(knapsack(id + 1, w), prices[id] + knapsack(id + 1, w - weights[id]))
}
Verificamos si el problema ya se precalculó
INTEGER N //Numero de objetos
INTEGER prices[] //precios de cada producto
INTEGER weights[] //pesos de cada producto
INTEGER memo[][]
INTEGER knapsack(INTEGER id, INTEGER w) {
IF (id == N || w == 0)
RETURN 0
IF (memo[id][w] != -1)
RETURN memo[id][w]
IF (weights[id] > w)
RETURN knapsack(id + 1, w)
ELSE
RETURN MAX(knapsack(id + 1, w), prices[id] + knapsack(id + 1, w - weights[id]))
}
Precalculamos y guardamos
INTEGER N //Numero de objetos
INTEGER prices[] //precios de cada producto
INTEGER weights[] //pesos de cada producto
INTEGER memo[][]
INTEGER knapsack(INTEGER id, INTEGER w) {
IF (id == N || w == 0)
RETURN 0
IF (memo[id][w] != -1)
RETURN memo[id][w]
IF (weights[id] > w)
memo[id][w] = knapsack(id + 1, w)
ELSE
memo[id][w] = MAX(knapsack(id + 1, w), prices[id] + knapsack(id + 1, w - weights[id]))
}
Precalculamos y guardamos
INTEGER N //Numero de objetos
INTEGER prices[] //precios de cada producto
INTEGER weights[] //pesos de cada producto
INTEGER memo[][]
INTEGER knapsack(INTEGER id, INTEGER w) {
IF (id == N || w == 0)
RETURN 0
IF (memo[id][w] != -1)
RETURN memo[id][w]
IF (weights[id] > w)
memo[id][w] = knapsack(id + 1, w)
ELSE
memo[id][w] = MAX(knapsack(id + 1, w), prices[id] + knapsack(id + 1, w - weights[id]))
RETURN memo[id][w]
}
Cambio de moneda
Dada una cantidad V de centavos, y una lista de n monedas existentes, determinar cual es la mínima cantidad de monedas que debe usarse para completar V.
- Sub-estructura óptima.
- Superposición de Problemas.
Planteamiento
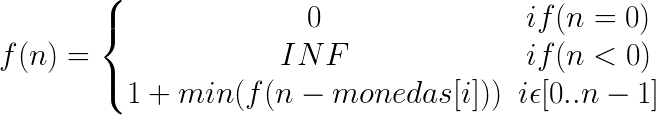
Solución Recursiva
INTEGER monedas[]
INTEGER change(INTEGER k) {
IF (k == 0)
RETURN 0
IF (k < 0)
RETURN INF
INTEGER rta = INF
FOR i IN RANGE[0, n - 1]
rta = MIN(rta, change(k - monedas[i]))
RETURN rta + 1
}
Añadiendo tabla DP
INTEGER monedas[n]
INTEGER memo[n] //Se inicializa en -1 o NULL
INTEGER change(INTEGER k) {
IF (k == 0)
RETURN 0
IF (k < 0)
RETURN INF
INTEGER rta = INF
FOR i IN RANGE[0, n - 1]
rta = MIN(rta, change(k - monedas[i]))
RETURN rta + 1
}
Verificando si ya ha sido calculado
INTEGER monedas[n]
INTEGER memo[MAX]
INTEGER change(INTEGER k) {
IF (k == 0)
RETURN 0
IF (k < 0)
RETURN INF
IF (memo[k] != -1)
RETURN memo[k]
INTEGER rta = INF
FOR i IN RANGE[0, n - 1]
rta = MIN(rta, change(k - monedas[i]))
RETURN rta + 1
}
Calculando y guardando
INTEGER monedas[n]
INTEGER memo[MAX]
INTEGER change(INTEGER k) {
IF (k == 0)
RETURN 0
IF (k < 0)
RETURN INF
IF (memo[k] != -1)
RETURN memo[k]
INTEGER rta = INF
FOR i IN RANGE[0, n - 1]
rta = MIN(rta, change(k - monedas[i]))
memo[k] = rta + 1
RETURN rta + 1
}