Geometría II

Polígonos convexos y concavos

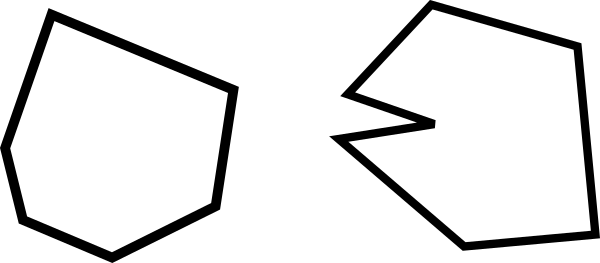
Saber si un polígono es convexo

                        
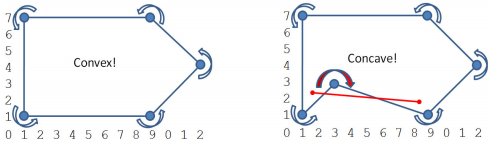
double cross(vec a, vec b) { return a.x * b.y - a.y * b.x; }

// Retorna true si el punto r está a la izquierda de pq
boolean ccw(point p, point q, point r) {
  return cross(toVec(p, q), toVec(p, r)) > 0; 
}
                        
                    

                        
boolean isConvex(ArrayList P) {
  int sz = (int)P.size();
  if (sz <= 3) return false; // un punto/sz=2 o una linea/sz=3 no son convexos
  boolean isLeft = ccw(P.get(0), P.get(1), P.get(2));
    for (int i = 1; i < sz-1; i++)
      if (ccw(P.get(i), P.get(i+1), P.get((i+2) == sz ? 1 : i+2)) != isLeft)
        return false; 
    return true; 
}
                        
                    

Envolvente convexa de un set de puntos

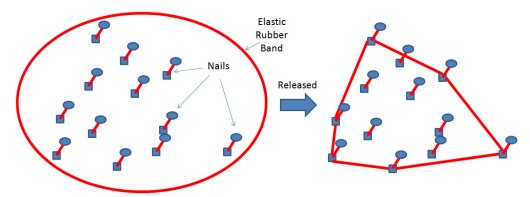
Se elige un pivot y los puntos se ordenan por sus angulos con el pivot

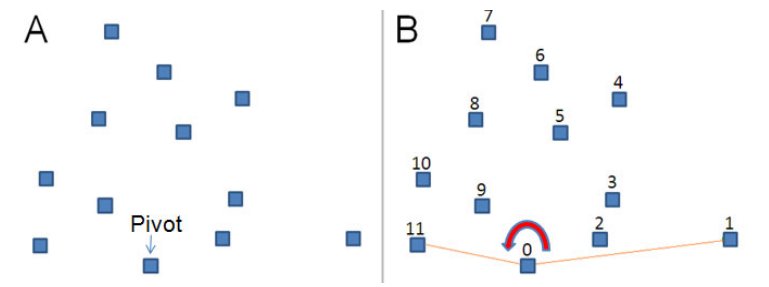
Se revisan los angulos punto por punto

                        
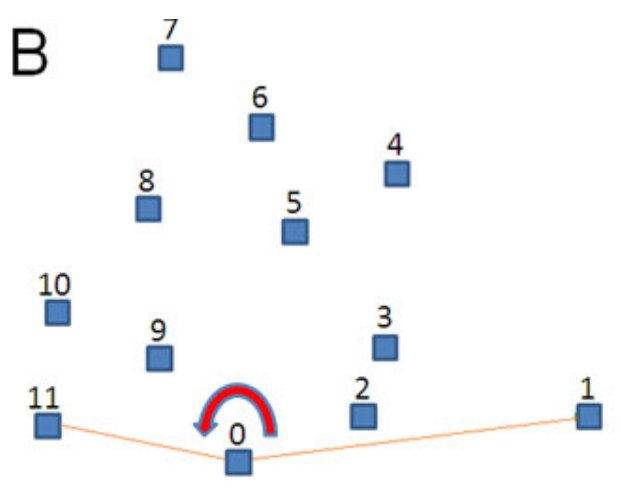
List CH(List P) {
  int i, j, n = (int)P.size();
  if (n <= 3) {
    if (P.get(0).compareTo(P.get(n-1)) != 0) P.add(P.get(0)); 
    return P;
  }

  // Primero se elige el pivot mas abajo a la izquierda
  int P0 = 0;
  for (i = 1; i < n; i++)
    if (P.get(i).y  < P.get(P0).y ||
      (P.get(i).y == P.get(P0).y && P.get(i).x > P.get(P0).x))
      P0 = i;

  // swap P[P0] con P[0]
  point temp = P.get(0); P.set(0, P.get(P0)); P.set(P0 ,temp); 

  // Ordenamos los puntos por su angulo con el pivot 
  pivot = P.get(0);
  Collections.sort(P, new Comparator(){
    public int compare(point a, point b) { 
      if (collinear(pivot, a, b))
        return dist(pivot, a) < dist(pivot, b) ? -1 : 1;
      double d1x = a.x - pivot.x, d1y = a.y - pivot.y;
      double d2x = b.x - pivot.x, d2y = b.y - pivot.y;
      return (Math.atan2(d1y, d1x) - Math.atan2(d2y, d2x)) < 0 ? -1 : 1;
    }
  });

  // Luego, test con ccw
  List S = new ArrayList();
  S.add(P.get(n-1)); S.add(P.get(0)); S.add(P.get(1));
  i = 2; 
  while (i < n) { 
    j = S.size() - 1;
    if (ccw(S.get(j-1), S.get(j), P.get(i))) S.add(P.get(i++)); 
    else S.remove(S.size() - 1); 
  }
  return S;
}