Matemáticas
- Sucesiones y secuencias
- Coeficiente binomial
- Conversiones
- BigInteger y BigDecimal
- Aritmética modular
Sucesiones y secuencias
Números Triangulares
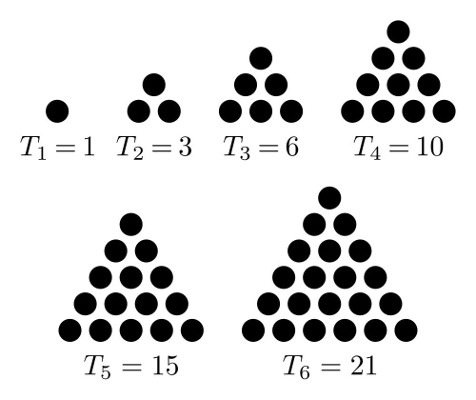
Números Triangulares
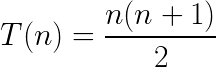
Fibonacci
0, 1, 1, 2, 3, 5, 8, 13, 21, 34...
fibo(0) = 0
fibo(1) = 1
fibo(n) = fibo(n - 1) + fibo(n - 2)
long fibo[] = new long[50];
fibo[0] = 0;
fibo[1] = 1;
for(int i = 2; i < 50; i++) {
fibo[i] = fibo[i - 1] + fibo[i - 2];
}
Números de catalan
Secuencia de números naturales que aparece en diferentes problemas de conteo.
1, 1, 2, 5, 14, 42, 132, 429, 1430...
De cuantas formas se pueden balancear n parentesis?.
| Número de parentesis | Formas de balancear | Número de formas |
| 0 | 1 | |
| 1 | () | 1 |
| 2 | ()(), (()) | 2 |
| 3 | ((())), ()()(), (())(), ()(()), (()()) | 5 |
Cálculo de un número de Catalán
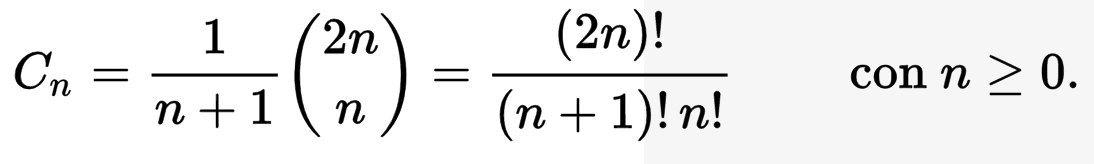
Cálculo de los números de Catalán
static int MAX = 30;
static long catalanNumbers[] = new long[MAX+1];
static void catalan(){
catalanNumbers[0] = 1;
for(int i = 1; i <= MAX; i++){
catalanNumbers[i] = (long)(catalanNumbers[i-1]*((double)(2*((2 * i)- 1))/(i + 1)));
}
}
Coeficientes binomiales
Número de formas en que se puede extraer subconjuntos a partir de un conjunto dado.
En una clase de 35 alumnos se quiere elegir un comité formado por tres alumnos. ¿Cuántos comités diferentes se pueden formar?

static long binomialCoefficient(long n, long r) {
if (r < 0 || n < r) {
return 0;
}
r = Math.min(r, n - r);
long ans = 1;
for (int i = 1; i <= r; i++) {
ans = ans * (n - i + 1) / i;
}
return ans;
}
Conversiones: De otra base a Entero
String bin = "111";
int dec = Integer.parseInt(bin, 2);
String octal = "777";
dec = Integer.parseInt(octal, 8);
String hexa = "FFF";
dec = Integer.parseInt(hexa, 16);
Conversiones: De entero a otras bases
int dec = 125;
String bin = Integer.toString(dec, 2);
String octa = Integer.toString(dec, 8);
String hexa = Integer.toString(dec, 16);
BigInteger
El mayor número que puede guardarse en un Long en java es: 9.223.372.036.854.775.807. Si se necesita almacenar u operar un número mas grande puede usarse BigInteger que teoricamente no tiene limite de tamaño.
IMPORTANTE: Usar SOLO cuando sea necesario. Es mucho mas lento que trabajar con int o long.
BigInteger num = new BigInteger("12333566576542341345465656");
BigInteger num2 = new BigInteger("1345657543245678765434565");
num = num.add(num2); // num = num + num2;
num = num.subtract(num2); // num = num - num2;
num = num.multiply(num2); // num = num * num2;
num = num.divide(num2); // num = num / num2;
System.out.println(num.toString());
BigDecimal
El mismo principio de BigInteger pero para valores reales. Corrige problemas de precisión con doubles, pero al igual que los BigInteger, son mas lentos que los datos primitivos. Usar SOLO cuando sea necesario.
Aritmética Modular
Muchos ejercicios dan como respuesta valores numericos muy altos. Por eso los enunciados indican que la salida debe darse en módulo de un número alto (Ej: mod 10^9 + 7). Es decir, lo que debemos imprimir será rta % 1000000007.
Cuando debamos trabajar con módulos como en este caso, debemos conocer las propiedades del módulo.
Propiedad Neutral
(a % b) % b = a % b
Ejemplo: (10 % 3) % 3 = 1 % 3 = 1
10 % 3 = 1
Propiedad asociativa de la multiplicación
(ab) % c = ((a % c)(b % c)) % c
Ejemplo: (10 * 5) % 3 = 50 % 3 = 2
((10 % 3) * (5 % 3)) % 3 = (1 * 2) % 3 = 2 % 3 = 2
Propiedad asociativa de la suma
(a + b) % c = ((a % c) + (b % c)) % c
Ejemplo: (10 + 5) % 3 = 15 % 3 = 0
((10 % 3) + (5 % 3)) % 3 = (1 + 2) % 3 = 3 % 3 = 0